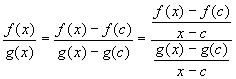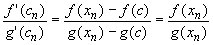6.5. Differentiable Functions
Theorem 6.5.15: l Hospital Rules
provided the limit on the right exists. The same result holds for one-sided limits.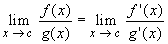
If f and g are differentiable and
 f(x) =
f(x) =
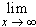 g(x) =
-
g(x) =
-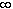 then
then
provided the last limit exists.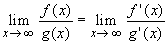
Proof:
The first part can be proved easily, if the right hand limit equals f'(c) / g'(c): Since f(c) = g(c) = 0 we have
Taking the limit as x approaches c we get the first result. However, the actual result is somewhat more general, and we have to be slightly more careful. We will use a version of the Mean Value theorem:
Take any sequence {xn} converging to c from above. All assumptions of the generalized Mean Value theorem are satisfied (check !) on [c, xn]. Therefore, for each n there exists a number cn in the interval (c, xn) such that
Taking the limit as n approaches infinity will give the desired result for right-handed limits. The proof is similar for left handed limits and therefore for 'full' limits.
The proof of the last part of this theorem is left as an exercise.
 Interactive Real Analysis
Interactive Real Analysis