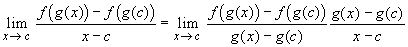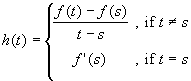6.5. Differentiable Functions
Theorem 6.5.7: Algebra with Derivatives
Product Rule: If f and g are differentiable at x = c then f(x) g(x) is differentiable at x = c and(f(x) + g(x)) = f'(x) + g'(x)
Quotient Rule: If f and g are differentiable at x = c, and g(c) # 0 then f(x) / g(x) is differentiable at x = c, and(f(x) g(x)) = f'(x) g(x) + f(x) g'(x)
Chain Rule: If g is differentiable at x = c, and f is differentiable at x = g(c) then f(g(x)) is differentiable at x = c, and( f(x) / g(x) ) =
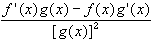
f(g(x)) = f'(g(x)) g'(x)
Proof:
These proofs, except for the chain rule, consist of adding and subtracting the same terms and rearranging the result. We will prove the product and chain rule, and leave the others as an exercise.
Product rule:
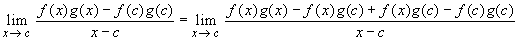 =
=
- =
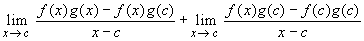 =
=
- =
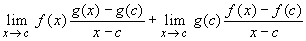 =
=
- = f(c) g'(c) + g(c) f'(c)
- =
Chain Rule: A 'quick and dirty' proof would go as follows:
Since g is differentiable, g is also continuous at x = c. Therefore, as x approaches c we know that g(x) approaches g(c). The first factor, by a simple substitution, converges to f'(u), where u = g(c). The second factor converges to g'(c). Hence, by our rule on product of limits we see that the final limit is going to be f'(u) g'(c) = f'(g(c)) g'(c), as required. But this 'simple substitution' may not be mathematically precise. Here is a better proof of the chain rule.
Define the function h(t) as follows, for a fixed s = g(c):
Since f is differentiable at s = g(c) the function h is continuous at s. We have
- f'(s) = h(s) =
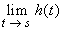
- f(t) - f(s) = h(t) (t - s)
Now we have, with t = g(x):
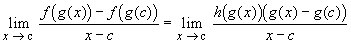 =
=
- =
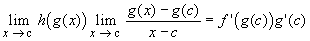
- =
which proves the chain rule. This is, of course, the rigorous version of the above 'simple substitution'.
Note that the chain rule and the product rule can be used to give a quick proof of the quotient rule.
 Interactive Real Analysis
Interactive Real Analysis