6.2. Continuous Functions
Theorem 6.2.9: Continuity and Uniform Continuity
If f is continuous on a compact domain D, then f is uniformly continuous in D.
Proof:
The first part of the proof is obvious. If |f(t) - f(s)| is small whenever |s - t| is small, regardless of the particular location of s and t, then in particular |f(x) - f( x0)| must be small when |x - x0| is small.
The second part is much more complicated, and relies on the structure
of compact sets on the real line. Recall that a set is compact
if every open cover has a finite subcover. We first want to define
a suitable open cover: pick an
 > 0. For every fixed
x0 in the compact set D there exists a
(possibly different)
> 0. For every fixed
x0 in the compact set D there exists a
(possibly different)
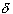 (x0) > 0
such that
(x0) > 0
such that
| f( x0) - f(x) | <if | x0- x | < 1/2
(x0)
where 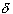 depends on
x0. Define
depends on
x0. Define
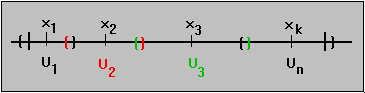
U(x0) = { x: |x0 - x| < 1/2(x0)} and U = { U(x0): x0 is contained in D}
Then U is an open cover of D, so by compactness can be reduced to a finite subcover. Suppose that the sets U1, U2, ..., Un cover the set D:
Let
= 1/2 min{
(x1),
(x2), ...
(xn)}
Since this is a minimum over a finite set, we know that
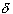 > 0. Now take any two numbers
t, s in D such that
|t - s| <
> 0. Now take any two numbers
t, s in D such that
|t - s| < 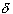 . Since the finite
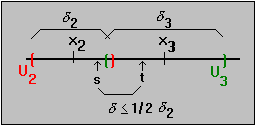
collection covers the compact set D we know that s is
contained in, say, U2. How far away from the center of
U2 is t then ?
. Since the finite
collection covers the compact set D we know that s is
contained in, say, U2. How far away from the center of
U2 is t then ?
By the choice of 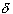 we know
that
we know
that
|t - x2| < |t - s| + |s - x2| <+ 1/2
(x2) < 1/2 (
( x2) +
( x2)) =
( x2)
Now we are almost done, because if |t - s| < 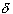 then
then
|f(t) - f(s)| < |f(t) - f( x2)| + |f( x2) - f(s)|
The first difference on the right is less than epsilon because
|t - x2| < 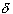 (x2).
The second one is also less than epsilon because s is contained in
the set U2. Hence, the difference on the left is less
than twice epsilon. But now it should be easy for you to modify the proof so
that we can arrive at
(x2).
The second one is also less than epsilon because s is contained in
the set U2. Hence, the difference on the left is less
than twice epsilon. But now it should be easy for you to modify the proof so
that we can arrive at
|f(t) - f(s)| <whenever |t - s| <
in D
That finishes the proof.
 Interactive Real Analysis
Interactive Real Analysis