6.6. A Function Primer
Cantor Function
Recall the definition of the Cantor set: Let
be the middle third of the interval [0, 1]. Let= [ 1/3, 2/3]
be the middle thirds of the intervals remaining after deleting= [ 1/9, 2/9],
= [ 7/9, 8/9 ]
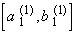 from [0, 1]. Let
from [0, 1]. Let
be the middle thirds of the intervals remaining after deleting= [2/27, 3/27],
= [7/27, 8/27],
= [19/27, 20/27],
= [ 25/27, 26,27]
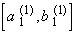 ,
,
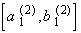 ,
and
,
and 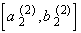 from [0, 1].
Continue in this fashion so that at the n-th stage we
have the intervals
from [0, 1].
Continue in this fashion so that at the n-th stage we
have the intervals
Then the complement of the union of all these intervals, ...,
, ...,
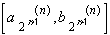
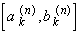 is the Cantor set without
the endpoints. Now define the following function
is the Cantor set without
the endpoints. Now define the following function
Then, for example, we have thatif t is in the interval
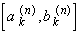
if 1/3
t
2/3
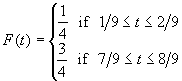
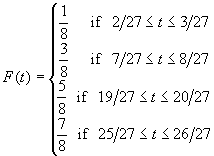
Then F(t) is defined everywhere in [0, 1] except at the Cantor set minus the end points 0, 1, 1/3, 2/3, 1/9, 2/9, 7/9, 8/9, ... If t is a number where F is not defined, then there exists an increasing sequence { xn } of these endpoints converging to t, and a decreasing sequence { xn' } of these endpoints converging to t. Since F is defined at those endpoints xn and xn', we define
F(t) =F(xn) =
F(xn')
Now we have defined completely the Cantor function. It has the following properties:
- F is defined everywhere in the interval [0, 1]
- F is not constant
- F is increasing
- F is continuous in the interval [0, 1]
- F is differentiable in the interval [0, 1]
- F' is zero at every interior point of the intervals
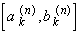
Proof
Some of these properties are obvious, and some require more thought. In particular, why does the above limit of endpoints exist ? That is a crucial point, because we used this limit to extend the function to the whole interval [0, 1]. For details and hints about the Cantor Function, please consult Kolmogorov and Fomin, p 334 ff.
 Interactive Real Analysis
Interactive Real Analysis