6.4. Topology and Continuity
Examples 6.4.2(b):
Let f(x) = 1 if x > 0 and f(x) = -1 if
x  0. Show that f
is not continuous by
0. Show that f
is not continuous by
 0. Show that f
is not continuous by
0. Show that f
is not continuous by
- finding an open set whose inverse image is not open.
- finding a closed set whose inverse image is not closed.
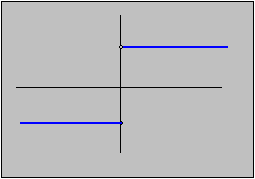
f(x) = 1 if x > 0 and f(x) = -1 if x
 0
0
The inverse image of the set [0,2] is the positive real axis without the origin. That set is open. We have found a closed set whose inverse image is not closed; therefore, the function is not continuous.
 Interactive Real Analysis
Interactive Real Analysis