6.5. Differentiable Functions
Examples 6.5.10(b):
If f is differentiable on R and
| f'(x) |  M
for all x, then
| f(x) - f(y) |
M
for all x, then
| f(x) - f(y) |  M | x - y |
for all numbers x, y.
M | x - y |
for all numbers x, y.
Functions that satisfy the inequality
 M
for all x, then
| f(x) - f(y) |
M
for all x, then
| f(x) - f(y) |  M | x - y |
for all numbers x, y.
M | x - y |
for all numbers x, y.
| f(x) - f(y) |for some constant M are called Lipschitz functions. Using those terms, we have to prove that if f is differentiable and uniformly bounded then it is a Lipschitz function.M | x - y |
Take any two number a, b. By the mean value theorem we know that there exists an x in (a, b) such that:
f'(x) =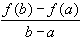
Taking absolute values on both sides and moving the denominator to the other side we have
| f(b) - f(a) | = | f'(x) | | b - a |Since f'(x) is uniformly bounded by M, we therefore have
| f(b) - f(a) |But that is exactly what we wanted to prove.M | b - a |
 Interactive Real Analysis
Interactive Real Analysis