6.2. Continuous Functions

Example 6.2.4(b):

If f(x) = x if x is rational and f(x) = 0 if x is irrational, prove that x is continuous at 0.
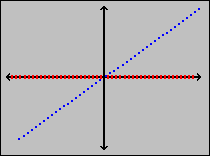
If one looks at this poor representation of the function, we see that it does not at all look continuous. But if {xn} is any sequence of numbers (rational or irrational) that converges to zero, then there exists an integer N such that |xn| < for n > N. But f(xn) is either zero or xn itself, and in any case we have
| f(xn) | | xn| <
That proves that the sequence of {xn)} converges to 0 = f(0), which proves that the function is continuous at zero.

As an exercise, prove that the function is not continuous for any other x.

Next | Previous | Glossary | Map