Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 6.1. Limits
• 6.2. Continuous Functions
• 6.3. Discontinuous Functions
• 6.4. Topology and Continuity
• 6.5. Differentiable Functions
• 6.6. A Function Primer
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

6.5. Differentiable Functions

Examples 6.5.6(a):

The function f(x) = | x | is continuous everywhere. Is it also differentiable everywhere ?

Back

We know that f is continuous. To check for differentiability, we have to employ the basic definition:

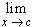
• f'(x) = 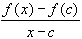= 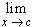( | x | - | c | ) / (x - c)
  • If c > 0 then x > 0 eventually. Then there is no need for the absolute value. The limit become +1.
  • If c < 0 then x < 0 eventually. The absolute values are resolved by an additional negative sign. The limit becomes -1.
  • If c = 0, then the left and the right-handed limits will be different (-1 and +1). Therefore, the function is not differentiable at 0.