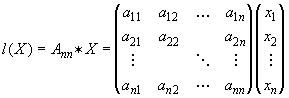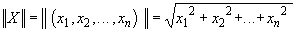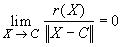6.5. Differentiable Functions
Examples 6.5.4(b):
Use the characterization of differentiability via approximation
by linear functions to define the concept of 'derivative' for
functions of n real variables.
As we have seen, we can not use the definition involving the limit
of the difference quotient as a definition of 'the derivative'
of a function of n real variables. Therefore, we want to try to
use the 'linear approximation' characterization to give us a workable
concept of derivatives in higher dimensions. First, recall that
a linear function in n variables is given as matrix multiplication:
where A is an n-by-n matrix with constant coefficients. As you recall, this is a linear map from n-dimensional space into itself. We can also define the concept of distance, or norm, in n-dimensional space as follows:
Now we can define 'the derivative' of a function f(X) of n-variables with range in Rn:
- f: Rn--> Rn is called 'differentiable'
at a point C in Rn if
there exists an n-by-n matrix A such that:
- f(X) = f(C) + A * (X - C) + r(X)
- where the remainder r(X) satisfies the condition
The matrix A is called the total derivative of the function f. It's coefficients, as you may recall from multi-dimensional calculus, are all possible partial derivatives of f at the point X = C.
We can define, in a similar fashion, the total differential of a function from n-dimensional into m-dimensional space, as long as we have the concept of a linear map and of a distance, or norm.
 Interactive Real Analysis
Interactive Real Analysis