6.2. Continuous Functions
Example 6.2.8(d):
- given any
 > 0 there
exists
> 0 there
exists 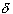 > 0 such that if
| t - s | <
> 0 such that if
| t - s | < 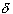 then | f(t)
- f(s) | <
then | f(t)
- f(s) | < 
If { xn} is a Cauchy sequence, there exists an integer N such that
- | xn - xj|
<
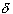 if n, j > N
if n, j > N
But then, by uniform continuity, we have that
- | f( xn) - f(xj) | <
 if
n, j > N
if
n, j > N
Therefore, the sequence { f( xn) } is again a Cauchy sequence.
Why will this argument will not work for a continuous function ? As an example, consider again the function f(x) = 1/x. It is continuous in the open interval (0, 1). Therefore, if we consider a sequence { xn} that converges to a fixed point inside (0, 1), the same argument as above would to show that { f( xn) } is also Cauchy. We can not use this argument, however, for a sequences that converge to 0, since f is not even defined at zero. On the other hand, we can find Cauchy sequences which converge to 0, without ever having to refer to the value of the function at the limit of the sequence.
 Interactive Real Analysis
Interactive Real Analysis