Interactive Real Analysis6.2. Continuous Functions
Example 6.2.8(c):
The function f(x) = x2 is
continuous on [0, 
).
Is it uniformly continuous there ?
Back
While this function is uniformly continuous on any interval
[0, N] (N any number) it is no longer uniformly continuous on
the interval [0, ).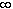
Is it uniformly continuous there ?
Back).
To prove this, take 
= 1. Note
that
| f(s) - f(t) | = | s - t | | s + t |
Can you see that if s = t + 
and
if t is sufficiently large (depending on the undetermined
)
then no matter what is chosen,
| f(s) - f(t) | > 1. That would prove that the function is
no longer uniformly continuous. The details are left as an exercise.
Note that this argument no longer works on a bounded interval [0, N]. Here we can not make t 'sufficiently large', since it can be no larger than N. And indeed, the function is uniformly continuous on those bounded intervals. Later we will show that any function that is continuous on a compact set is necessarily uniformly continuous.