6.2. Continuous Functions
Example 6.2.8(b):
This function (as you could guess from its graph) is uniformly continuous on the closed interval [0, 1]. To prove it, note that
| f(t) - f(s) | = | t - s | | t + s | < | t - s | 2
because s and t are in the interval [0, 1]. Hence,
given any  > 0 we can simply choose
> 0 we can simply choose
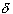 =
=  / 10
(or something similar) to prove uniform convergence. Can you fill in the details ? A similar
argument, incidentally, would work on the interval [0, N] for any number
N, but it would fail for the interval
[0,
/ 10
(or something similar) to prove uniform convergence. Can you fill in the details ? A similar
argument, incidentally, would work on the interval [0, N] for any number
N, but it would fail for the interval
[0, 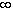 ). So, if this function then
uniformly continuous on the interval
[0,
). So, if this function then
uniformly continuous on the interval
[0, 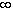 ) ? That's the next example.
) ? That's the next example.
 Interactive Real Analysis
Interactive Real Analysis