MathCS.org - Java: ZMap Quick Guide

zMap: Quick Guide

The ZMap applet lets you investigate mapping properties of user-defined complex functions. When you start the program you will see two coordinate systems: one on the left representing the domain and one on the right representing the range. You can enter a function defined in terms of z, such as z², to investigate. Then you can specify curves in the domain (horizontal lines, vertical lines, radii, arcs, or circles) to see how your function transforms them.

If you click the above example, the function f(z) = z² has been pre-selected, together with two horizontal lines through z = 1/2 i and z = i. You will see that both lines are mapped to "left-right" parabolas, as shown before.

Question: Into what curves does the complex function f(z) = z² transform vertical lines such as the vertical line through z = 2?

Answer: Before we check the answer mathematically, we use ZMap to come up with a good guess:

Start ZMap by clicking on the above applet button.
The applet should appear, with two horizontal lines and their images visible
Check the V-lines and uncheck the H-lines checkboxes.
You now see several vertical lines and their images, while the horizontal lines are no longer visible.
Click on the Rectangle Options button
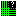
A dialog window will appear where you can adjust the parameters for your lines
Adjust the parameters so that the Horizontal Lines go from -10 to 10, while the Vertical Lines go from 1 to 2. Also set the number of lines for the vertical lines to 2 (it does not matter how many horizontal lines you enter). Then click on Okay (or Apply).
You should now see that vertical lines are mapped to left-right parabolas, opening to the left
To zoom out in the range, click Range zoom out twice.
You should now see see the entire parabolas in the range. If you move the mouse over the y-intercept on the range you can see that the y-intercepts of the right-most parabola are z = -8 i and z = +8 i, approximately.
To recenter (pan) the range, double-click on the origin (0,0) of the coordinate system in the range.
The coordinate system in the range is panned so that the origin is now in the center of the window. You can undo all zoom/pan operations by clicking the appropriate undo buttons or , or by right-clicking on domain or range.
To determine where an individual point in the domain is mapped, hold down the CTRL-key and click once on the point in the domain where the blue vertical line intersects the real (x) axis.
You will see a yellow dot appear in the domain where you CTRL-clicked as well as the image of that point in the range. You can see that the point with imaginary part zero is mapped to a point also with imaginary part zero. You could now conjecture that our map takes the real axis onto the real axis - is that true?

Of course we should verify this mathematically: a vertical line through z = 2 is given by l(t) = 2 + i t. Thus:

f(z) = f(2 + i t) = 4 - t² + i 4t

But that is equivalent to

x = 4 - 1/16 y²

which is, indeed, a left-right parabola, opening to the left, with vertex at x = 4, and y-intercepts at y = -8 and y = +8. Thus, our rigorous math confirms our guess.