5.1. Open and Closed Sets
Proposition 5.1.7: Boundary, Accumulation, Interior, and Isolated Points
- Let S
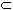 R.
Then each point of S is either an interior point or a boundary
point.
R.
Then each point of S is either an interior point or a boundary
point.
- Let S
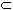 R.
Then bd(S) = bd(R \ S).
R.
Then bd(S) = bd(R \ S).
- A closed set contains all of its boundary points. An open set
contains none of its boundary points.
- Every non-isolated boundary point of a set S
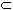 R is an accumulation
point of S.
R is an accumulation
point of S.
- An accumulation point is never an isolated point.
 Interactive Real Analysis
Interactive Real Analysis