5.1. Open and Closed Sets
Definition 5.1.1: Open and Closed Sets
A set
U 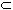 R
is called open, if for each
x
R
is called open, if for each
x  U
there exists an
U
there exists an
 > 0
such that the interval
( x -
> 0
such that the interval
( x -  ,
x +
,
x +  )
is contained in U. Such an interval is often called an
)
is contained in U. Such an interval is often called an
 -neighborhood of x,
or simply a neighborhood of x.
-neighborhood of x,
or simply a neighborhood of x.
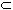 R
is called open, if for each
x
R
is called open, if for each
x  U
there exists an
U
there exists an
 > 0
such that the interval
( x -
> 0
such that the interval
( x -  ,
x +
,
x +  )
is contained in U. Such an interval is often called an
)
is contained in U. Such an interval is often called an
 -neighborhood of x,
or simply a neighborhood of x.
-neighborhood of x,
or simply a neighborhood of x.
A set F is called closed if the complement of F, R \ F, is open.
 Interactive Real Analysis
Interactive Real Analysis