5.2. Compact and Perfect Sets
Example 5.2.13(c): Properties of the Cantor Set
The definition of the Cantor set is as follows: letA0 = [0, 1]and define, for each n, the sets An recursively as
An = An-1 \Then the Cantor set is given as: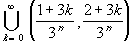
C =To be more specific, we have:An
A0 = [0, 1]That is, at the n-th stage (n > 0) we remove 2 n-1 intervals from each previous set, each having length 1 / 3 n. Therefore, we will remove a total length of
A1 = [0, 1] \ (1/3, 2/3)
A2 = A1 \ [(1/9, 2/9)(7/9, 8/9)] =
[0,1] \ (1/3, 2/3) ) \ (1/9, 2/9) \ (7/9, 8/9)
...
from the unit interval [0, 1]. Since we remove a set of total length 1 from the unit interval, the length of the remaining Cantor set must be 0.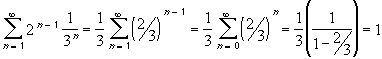
The Cantor set contains uncountably many points because it is a perfect set.
 Interactive Real Analysis
Interactive Real Analysis