4.2. Convergence Tests
Comparison Test
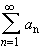 converges absolutely, and
converges absolutely, and
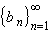 is a sequence of numbers for which
| bn |
is a sequence of numbers for which
| bn |  | an |
for all n > N. Then the series
| an |
for all n > N. Then the series
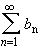 converges absolutely as well.
converges absolutely as well.
If the series 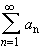 converges to positive infinity, and
converges to positive infinity, and
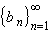 is a sequence
of numbers for which
an
is a sequence
of numbers for which
an  bn
for all n > N. Then the series
bn
for all n > N. Then the series
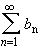 also diverges.
also diverges.
| b n |for all n. then just sum both sides to see what you get formally:| a n |
Then: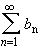

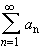
- If the left sides equals infinity, so must the right side.
- If the right side is finite, the left side also converges.
The proof, at first glance, seems easy: Suppose that
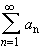 converges absolutely, and
| b n |
converges absolutely, and
| b n |  | a n |
for all n. For simplicity, assume that all terms in
both sequences are positive. Let
| a n |
for all n. For simplicity, assume that all terms in
both sequences are positive. Let
S N =Then we have thatand T N =
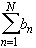
T NSince the left side is a convergent sequence, it is in particular bounded. Hence, the right side is also a bounded sequence of partial sums. Therefore it converges.SN
This proof wrong, because it does show that the sequence of partial sums is bounded but it is not necessarily true that a bounded series also converges - as we know.
However, this proof, slightly modified, does work: Again, assume
that all terms in both sequences are positive. Since
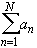 converges, it satisfies the Cauchy criterion:
converges, it satisfies the Cauchy criterion:
|if m > n > N. Since | b n || <

 | a n |
we then have
| a n |
we then have
|if m > n > N. Hence|
|
| <

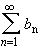 satisfies the Cauchy criterion, and therefore converges.
satisfies the Cauchy criterion, and therefore converges.
The proof for divergence is similar.
 Interactive Real Analysis
Interactive Real Analysis converge or diverge ?
converge or diverge ?
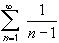 converge or diverge ?
converge or diverge ?