4.1. Series and Convergence
Theorem: Absolute Convergence implies Convergence
If a series 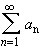 converges
absolutely, it converges in the ordinary sense. The converse is not true.
converges
absolutely, it converges in the ordinary sense. The converse is not true.
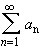 converges
absolutely, it converges in the ordinary sense. The converse is not true.
converges
absolutely, it converges in the ordinary sense. The converse is not true.
Suppose 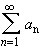 is absolutely convergent. Let
is absolutely convergent. Let
Tj = |a1| + |a2| + ... + |aj|
be the sequence of partial sums of absolute values, and
Sj = a1 + a2 + ... + aj
be the "regular" sequence of partial sums. Since the series converges absolutely, there exists an integer N such that:
| Tn - Tm| = |an| + |an-1| + ... + |am+2| + |am+1| <
if n > m > N. But we have by the triangle inequality that
| Sn - Sm| = | an + an-1 + ... + am+2 + am+1 |
|an| + |an-1| + ... + |am+2| + |am+1| = | Tn - Tm | <

Hence the sequence of regular partial sums {Sn} is Cauchy and therefore must converge (compare this proof with the Cauchy Criterion for Series).
The converse is not true because the series
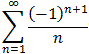 converges, but the
corresponding series of absolute values
converges, but the
corresponding series of absolute values
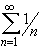 does not converge.
does not converge.
 Interactive Real Analysis
Interactive Real Analysis