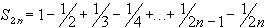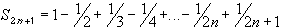Alternating Series Test
Examples 4.2.20(a):
The Alternating Harmonic Series:
The series
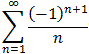 is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
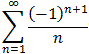 is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
is called the Alternating Harmonic series. It converges but
not absolutely, i.e. it converges conditionally.
Proof:
There are many proofs of this fact. For example. the series of absolute values is a p-series with p = 1, and diverges by the p-series test. The original series converges, because it is an alternating series, and the alternating series test applies easily. However, here is a more elementary proof of the convergence of the alternating harmonic series.We already know that the series of absolute values does not converge by a previous example. Hence, the series does not converge absolutely. As for regular convergence, consider the following two partial sums:
- S 2n+2 - S 2n = 1 / (2n+1) - 1 / (2n+2) > 0
- S 2n+3 - S 2n+1 = - 1 / (2n+2) + 1/ (2n+3) < 0
- { S 2n } is monotone increasing
- { S 2n+1 } is monotone decreasing
- S 2n
 1 for all n
1 for all n
- S 2n+1
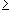 0 for all n
0 for all n
- lim S 2n = L and lim S 2n+1 = M
| M - L | = | lim (S 2n+1 - S 2n) | = 1 / (2n+1)which converges to zero. Therefore, M = L, i.e. both subsequences converge to the same limit. But this common limit is the same as the limit of the full sequence, because: given any
 > 0 we have
> 0 we have
- there exists an integer N such that
| L - S 2n | <
 if n > N
if n > N
- there exists an integer M such that
| L - S 2n+1 | <
 if n > M
if n > M
 > 0 we have
> 0 we have
| L - S n | <for n > K, because n is either even or odd. Hence, the alternating harmonic series converges conditionally.
 Interactive Real Analysis
Interactive Real Analysis