Abel Convergence Test
Examples 4.2.18(a):
We already know that the series does not converge absolutely (why ?). As for convergence, let us verify the conditions for Abel's test:
First, let
{ a n } = { (-1) n }and
{ b n } = { 1 / n }Then the sequence of partial sums of a n's is clearly bounded (by what number ?), and the sequence { b n } is decreasing and convergent to zero. Hence, Abel's test applies, showing that the series converges.
Therefore, the series converges conditionally.
 Interactive Real Analysis
Interactive Real Analysis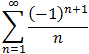 converges conditionally.
converges conditionally.