3.5. Special Sequences
Definition 3.5.4: n-th Root Sequence
n-th Root sequence with a = 3
Proof:
- Case a > 1:
- If a > 1, then for n large enough we have
1 < a < n. Taking roots on both sides
we obtain
1 <
But the right-hand side approaches 1 as n goes to infinity by our statement of the root-n sequence. Then the sequence {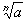 <
<
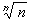
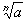 }
must also approach 1, being squeezed between 1 on both sides (Pinching
theorem).
}
must also approach 1, being squeezed between 1 on both sides (Pinching
theorem).
- Case 0 < a < 1:
- If 0 < a < 1, then (1/a) > 1. Using the first part
of this proof, the reciprocal of the sequence
{
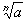 } must converge to one,
which implies the same for the original sequence.
} must converge to one,
which implies the same for the original sequence.
 Interactive Real Analysis
Interactive Real Analysis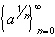 n-th Root Sequence: This sequence converges to 1 for any
a > 0.
n-th Root Sequence: This sequence converges to 1 for any
a > 0.