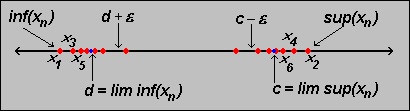
3.4. Lim Sup and Lim Inf
Proposition 3.4.4: Characterizing lim sup and lim inf
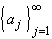 be an
arbitrary sequence, and let
c = lim sup aj and
d = lim inf aj. Then
be an
arbitrary sequence, and let
c = lim sup aj and
d = lim inf aj. Then
- there is a subsequence converging to c
- there is a subsequence converging to d
-
d
 lim inf
lim inf 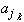
 lim sup
lim sup 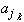
 c
for any subsequence
{
c
for any subsequence
{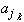 }
}
 > 0 there are arbitrary
large j such that
aj > c -
> 0 there are arbitrary
large j such that
aj > c -  and arbitrary large k such that
ak < d +
and arbitrary large k such that
ak < d +  .
.
Proof:
First let's assume that c = lim sup{aj} is finite, which implies that the sequence {aj} is bounded. Recall the properties of the sup (and inf) for sequences:If a sequence is bounded above, then given anyNow take any> 0 there exists at least one integer k such that ak > c -

 > 0. Then
> 0. Then
Ak = sup{ak, ak+1, ...}so by the above property there exists an integer jk > k such that
Ak >or equivalently> Ak -
/ 2
| Ak -We also have by definition that Ak converges to c so that there exists an integer N such that| <
/ 2
| Ak - c | <But now the subsequence {/ 2
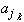 }
is the desired one, because:
}
is the desired one, because:
|if jk > N. Hence, this particular subsequence of {an} converges to c.- c | = |
- Ak + Ak - c |
|
- Ak | + | Ak - c |
</ 2 +
/ 2 =

The proof to find a subsequence converging to the lim inf is similar and is left as an exercise.
Statement (3) is pretty simple to prove: For any sequence we always have that
inf{ak, ak+1, ... }Taking limits on both sides gives lim inf(an)sup{ak, ak+1, ... }
 lim sup(an)
for any sequence, so it is true in particular for any subsequence.
lim sup(an)
for any sequence, so it is true in particular for any subsequence.
Next take any subsequence of {an}. Then:
inf(ak, ak+1, ...)because an infimum over more numbers (on the left side) is less than or equal to an infimum over fewer numbers (on the right side). But theninf(
,
, ...)
dThe proof of the inequality lim sup(lim inf(
)
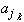 )
)
 c
is similar. Taking all pieces together we have shown that
c
is similar. Taking all pieces together we have shown that
dfor any subsequence {lim inf
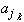
lim sup
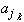
c
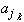 },
as we set out to do.
},
as we set out to do.
It remains to show that given any
 > 0 there are
arbitrary large j such that
aj > c -
> 0 there are
arbitrary large j such that
aj > c -  (as well as the corresponding statement for the lim inf d).
(as well as the corresponding statement for the lim inf d).
But previously we have found a subsequence
{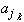 } that
converges to c so that there exists an integer
N such that
} that
converges to c so that there exists an integer
N such that
|if k > N. But that means that -- c | <

 <
<
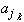 - c
<
- c
<
 which implies that
which implies that
c -as long as k > N. But that of course means that there are arbitrarily large indices - namely those jk for which k > N - with the property that<
< c +

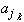 >
c -
>
c -  as required. Hence, we have shown the last statement involving the
lim sup, and a similar proof would work for the
lim inf.
as required. Hence, we have shown the last statement involving the
lim sup, and a similar proof would work for the
lim inf.
All our proofs rely on the fact that the lim sup and lim inf are bounded. It is not hard to adjust them for unbounded values, but we will leave the details as an exercise.
Contributed to this page: Thomas Wollmann
 Interactive Real Analysis
Interactive Real Analysis