Interactive Real Analysis3.1. Sequences
Definition 3.1.2: Convergence
A sequence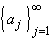 
of real (or
complex) numbers is said to converge to a real (or complex) number
c if for every 
> 0
there is an integer N > 0 such that if j > N then
| aj - c | < .
The number c is called the limit of the sequence
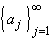and we sometimes write
aj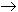 
c.
Context
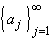of real (or
complex) numbers is said to converge to a real (or complex) number
c if for every > 0
there is an integer N > 0 such that if j > N then
| aj - c | < .
The number c is called the limit of the sequence
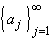and we sometimes write
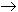aj c.
If a sequence 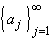does not
converge, then we say that it diverges.
Context