3.3. Subsequences
Examples 3.3.2(b):
Take the sequence
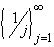 .
Extract three different subsequences of your choice and look
at the convergence behavior of these subsequences.
.
Extract three different subsequences of your choice and look
at the convergence behavior of these subsequences.
The sequence in question is:
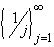 .
Extract three different subsequences of your choice and look
at the convergence behavior of these subsequences.
.
Extract three different subsequences of your choice and look
at the convergence behavior of these subsequences.
which converges to zero. Now let us extract some subsequences:= {1, 1/2, 1/3, 1/4, 1/5, 1/6, ... }
Extracting the even terms yields the subsequence
{1/2, 1/4, 1/6, 1/8, 1/10, ...}which converges to zero (prove it !).
Extracting the odd terms yields the subsequence
{1, 1/3, 1/5, 1/7, 1/9, ...}which converges to zero (prove it !).
Extracting every third member yields the sequence
{1, 1/4, 1/7, 1/10, 1/13, ...}which converges to zero (prove it !).
Hence, all three subsequences converge to zero. This is an illustration of a general result: if a sequence converges to a limit L then every subsequence extracted from it will also converge to that limit L.
 Interactive Real Analysis
Interactive Real Analysis