1.1. Notation and Set Theory
Definition 1.1.1: Sets and Operations on Sets
A set is a collection of objects chosen from some universe. The universe
is usually understood from the context. Sets are denoted by capital letters or curly
brackets.
- A
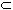 B:
A is a subset of B means that every element in A
is also contained in B.
B:
A is a subset of B means that every element in A
is also contained in B.
- A
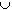 B:
A union B is the set of all elements that are either in A or in
B or in both sets.
B:
A union B is the set of all elements that are either in A or in
B or in both sets.
- A
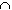 B:
A intersection B is the set of all elements that are in both sets A
and B.
B:
A intersection B is the set of all elements that are in both sets A
and B.
- A \ B: A minus B are all elements from A that are not in B.
- comp(A): The complement of A consists of all elements that are not in A.
- Two sets are disjoint if A
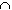 B = 0 (the empty set)
B = 0 (the empty set)
- Two sets A and B are equal if
A
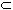 B and
B
B and
B 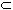 A
A
 Interactive Real Analysis
Interactive Real Analysis