7.4. Lebesgue Integral
Proposition 7.4.10: Properties of the Lebesgue Integral
Suppose f and g are two bounded, Lebesgue integrable
functions defined on a measurable set E with finite measure. Then:
-
 E c f(x) + d g(x) dx =
c
E c f(x) + d g(x) dx =
c  E f(x) dx +
d
E f(x) dx +
d  E g(x) dx
E g(x) dx
- If A and B are disjoint measurable subsets of
E then
 A
A 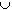 B f(x) dx =
B f(x) dx =
 A f(x) dx +
A f(x) dx +
 B f(x) dx
B f(x) dx
- If f(x) = g(x) for all x in E
except possibly on a set of measure zero then
 E f(x) dx =
E f(x) dx =
 E g(x) dx
E g(x) dx
- If f(x)
 g(x) for all x
in E except possibly on a set of measure zero then
g(x) for all x
in E except possibly on a set of measure zero then
 E f(x) dx
E f(x) dx

 E g(x) dx
E g(x) dx
 Interactive Real Analysis
Interactive Real Analysis