7.2. Integration Techniques
Example 7.2.2: Standard Antiderivatives
Find the following antiderivatives:
For each function to integrate we need to come up with another function
whose derivative is the integrand. Therefore we guess a function
F, then differentiate it (for which there are fixed rules).
If indeed F' is equal to the integrand, we have found an
antiderivative and we are done.
(a) xr dx
(b) 1/x dx
(c) ex dx
(d) sin(x) dx
(e) cos(x) dx
(f) tan(x) dx
(g) (h) (i)
Actually, if we can find one antiderivative F of a function f, the function F(x) + c is also an antiderivative. To simplify notation, we will be content with finding one antiderivative and not note the arbitrary constant (which drops out anyway when evaluating F(b) - F(a)).
(a)  xr dx
xr dx
We need a function whose derivate is f(x) = xr. Since differentiating a power reduces it by one, finding the opposite might mean increasing the power by one. Therefore, our first guess for the antiderivative is F(x) = xr+1. A quick check shows:(b)which has the correct power but an incorrect coefficient. Therefore we guess again: let F(x) = 1/r+1 xr+1, where r # -1. Thenxr+1 = 1/r+1 xr
F'(x) = r+1/r+1 xr = xrso that we have found the correct antiderivative, valid for all x and for r # -1:xr dx = 1/r+1 xr+1
 1/x dx
1/x dx
This is x to the power -1, which we had to exclude from the example above. Simple power functions, therefore, are not sufficient as antiderivatives and we need to resort to more exotic functions. Thinking a little we remember that there is the natural logarithm ln whose derivative is(c)But that function is only defined for positive x. On the other hand, if x is negative then -x is positive, andln(x) = 1/x
again. Thereforeln(-x) = -1/(-x) = 1/x
where the bounds of integration must either both be positive or both be negative, i.e. the point x = 0 can not be inside the integration interval [a, b].1/x dx = ln( |x| )
 ex dx
ex dx
The distinguishing feature of the exponential function is that it is its own derivative. But then it is also its own antiderivative, so that(d)ex dx = ex
 sin(x) dx
sin(x) dx
The close cousin of the trig function sin is of course the cos, whose derivative is -sin. But then:(e)sin(x) dx = -cos(x)
 cos(x) dx
cos(x) dx
This is similar to above, and we can guess the answer right away (and verify it by differentiating the right side to obtain the integrand):(f)cos(x) dx = sin(x)
 tan(x) dx
tan(x) dx
Now it gets complicated. No simple function has the tan as its derivative, so we seem to be stuck. But then tan(x) = sin(x) / cos(x), which at first glance does not help much. But in terms of differentiation, the top function happens to be the derivative of the bottom function (except for a negative sign), so that we - after being struck by intuition - come up with a function F(x) = ln(cos(x)). Differentiating gives F'(x) = -sin(x) / cos(x), which is almost correct. Adjusting for the minus sign we have as our final answer:(g)where the integration interval [a, b]tan(x) dx = - ln( cos(x) )
( -
/2,
/2). (We will soon see a technique called substitution that can clarify the intuitive flash we had)
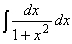
This is again tricky. We could guess for quite a while here, not much seems to work. But then - again an intuitive wonder - we remember the arctan function, whose derivative is just what we need:(h)arctan(x) = 1/ 1 + x2 so that:
= arctan(x)
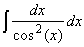
Well, tricky again. But we already tried to find the antiderivative of the tan in one of the earlier examples. While we were trying to find that answer, we might have computed the derivative of the tan, which was at that time not helpful. But it works now, as a quick application of the quotient rules shows:(i)Therefore: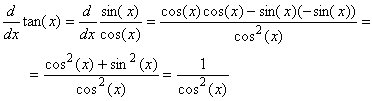
= tan(x)
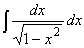
Now it gets to be really exotic. We have already seen that the derivative of the arctan function yields an expression with an x2 in the denominator. Therefore we should recall the derivatives of the other two (less frequently used) inverse trig functions arccos and arcsin.Therefore we have: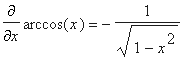
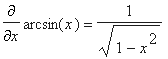 Incidentally, can you prove that the derivative for the arcsin is indeed as shown above (or for the arccos or arctan, for that matter)?
Incidentally, can you prove that the derivative for the arcsin is indeed as shown above (or for the arccos or arctan, for that matter)?= arcsin(x)
 Interactive Real Analysis
Interactive Real Analysis