7.4. Lebesgue Integral
Example 7.4.4(c): Lebesgue Integral for Simple Functions
Find the Lebesgue integral of the Dirichlet function restricted to
[0, 1] and of the characteristic function of the Cantor
middle-third set.
If Q is the set of all rational numbers, then the Dirichlet
function restricted to [0, 1] is the characteristic function
of A = Q 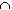 [0, 1].
The set A is a subset of Q, hence A is
measurable and m(A) = 0. Therefore:
[0, 1].
The set A is a subset of Q, hence A is
measurable and m(A) = 0. Therefore:
The Cantor middle-third set C is also measurable with measure 0. Therefore, by definitionXA(x) dx = m(A) = 0
Note that the Riemann integral of either function does not exist (which we have shown for the Dirichlet function, and leave as an exercise for the characteristic function of the Cantor set).XC(x) dx = m(C) = 0
 Interactive Real Analysis
Interactive Real Analysis