7.3. Measures
Example 7.3.5(a): Properties of Outer Measure
Show that the outer measure of a single point is 0, and the outer measure
of a countable set is also 0.
To find the measure of the set A = {a} is easy: since
(a-1/n, a+1/n) covers A we know that
m*(A)for all integers n. But then m*(A) = 0.m*(a-1/n, a+1/n) = 2/n
Now let A = 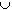 { an }.
Using subadditivity we know that
{ an }.
Using subadditivity we know that
m*(A)But each outer measure on the right is zero by the first part, so that m*(A) = 0.
m*(an)
 Interactive Real Analysis
Interactive Real Analysis