Interactive Real Analysis

• Real Analysis
• 1. Sets and Relations
• 2. Infinity and Induction
• 3. Sequences of Numbers
• 4. Series of Numbers
• 5. Topology
• 6. Limits, Continuity, and Differentiation
• 6.1. Limits
• 6.2. Continuous Functions
• 6.3. Discontinuous Functions
• 6.4. Topology and Continuity
• 6.5. Differentiable Functions
• 6.6. A Function Primer
• 7. The Integral
• 8. Sequences of Functions
• 9. Historical Tidbits
• Java Tools

6.2. Continuous Functions

Proposition 6.2.3: Continuity preserves Limits

If f is continuous at a point c in the domain D, and {x_n} is a sequence of points in D converging to c, then 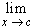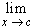f(x) = f(c).

If 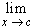f(x) = f(c) for every sequence {x_n} of points in D converging to c, then f is continuous at the point c.

Context

Proof:

The proof is very similar to the previous result about the equivalence of the two definitions of limits for a function. It is therefore left as an exercise. It would be good practice to see if you can modify the previous proof and adapt it to this result.