6.4. Topology and Continuity
Proposition 6.4.4: Images of Compact and Connected sets
- the image of every compact set is again compact.
- the image of every connected set is again connected.
Proof:
1. Note that the image of a closed set is not necessarily closed for continuous functions, and the image of a bounded set is not necessarily bounded. However, the image of a close and bounded set is again closed and bounded (under continuous functions). Despite this, the proof is fairly easy: Recall that a set D is compact if every open cover of D can be reduced to a finite subcover.
Let A be an open cover of the set f(D). Since f is continuous, the collection
- {f-1(U):
U
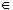 A}
A}
is a collection of open sets that cover D. Since D is compact, this collection can be reduced to a finite subcover, say:
- f-1( U1), f-1( U2), ..., f-1( Un),
But then the sets U1, U2, ..., Un cover the set f(D). Hence, every open cover of f(D ) can be reduced to a finite subcover. Therefore, f(D ) is compact.
Note: We have used the fact that the inverse image of open sets is open. That, however, is only true if the original domain D of the function is also open. Can you modify this proof so that it still works for a not necessarily open domain D ?
2. This prove is again simple. The idea is as follows:
suppose U 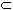 D
is connected, but f(U) is not connected. Then
D
is connected, but f(U) is not connected. Then
- f(U ) = A
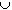 B
with A, B open and disjoint
B
with A, B open and disjoint
Since f is continuous, f-1(A) and f-1(B) are both open. They are clearly disjoint, and their union makes up all of U. But then U is not connected, which is a contradiction. Thus, the image of every connected set under a continuous function is connected.
Note: Just as before, this proof is not completely correct. It does reflect the major idea, but some technicalities are missing. Why is this proof technically not correct ? Can you fix it ?
 Interactive Real Analysis
Interactive Real Analysis