6.4. Topology and Continuity
Examples 6.4.3:
Is it true that if f is continuous, then the image of an open
set is again open ? How about the image of a closed set ?
This is true for inverse images but not for images. Consider the example of a parabola, which certainly represents a continuous function:
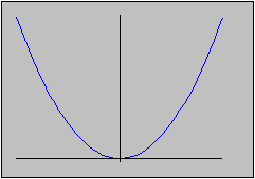
f(x) = x2
To find a counterexample for images of closed sets, let's look at the following function:
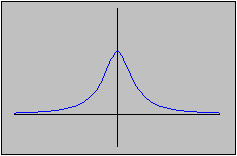
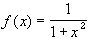
 )
is the set (0, 1]. Therefore we have found a closed set whose
image under a continuous function is not closed (nor open).
)
is the set (0, 1]. Therefore we have found a closed set whose
image under a continuous function is not closed (nor open).
 Interactive Real Analysis
Interactive Real Analysis