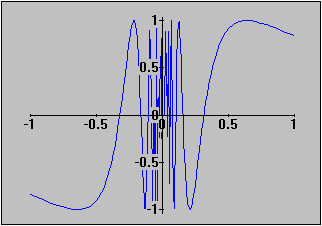
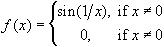Interactive Real Analysis6.3. Discontinuous Functions
Examples 6.3.4(c):
Prove that f(x) has a discontinuity of second kind at x = 0
Back
This function is more complicated. Consider the sequence
xn = 1 / (2 n  |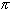
 |
Back
).
As n goes to infinity, the sequence converges to zero from the right.
But f( xn) = sin(2 n 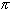) = 0
for all k. On the other hand, consider the sequence
xn = 2 / ( (2n+1) ).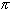
Again, the sequence converges to zero from the right as n goes
to infinity. But this time
f( xn) = sin( (2n+1) 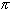/ 2)
which alternates between +1 and -1. Hence, this limit does
not exist. Therefore, the limit of f(x) as x approaches zero from
the right does not exist.
Since f(x) is an odd function, the same argument shows that the limit of f(x) as x approaches zero from the left does not exist.
Therefore, the function has an essential discontinuity at x = 0.